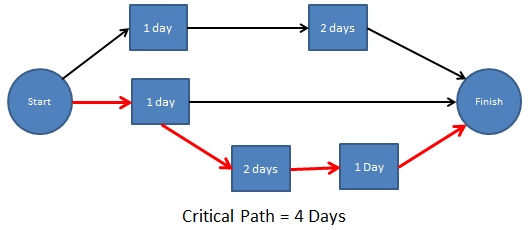
The Critical Path Method (CPM) is a way to determine the critical path of a schedule. The critical path is the longest path of scheduled activities that must be met to execute a project. This is important for Program Managers (PM) to know since any problems on the critical path can prevent a project from moving forward and being delayed. Earned Value Management (EVM) analysis focuses on critical and near-critical paths to identify cost and schedule risks. Unlike the critical path, other schedule paths might have slack time to avoid delaying the entire project. There might be multiple critical paths on a project. The method is used with Program Evaluation and Review Techniques (PERT).
Definition: The Critical Path Method (CPM) is a scheduling technique to determine a schedules critical path by calculating the longest path of planned activities to the end of the project and the earliest and latest that each activity can start and finish without making the project longer.
Critical Path Method (CPM) Goal
The goal of the Critical Path Method (CPM) is to determine the critical path of a schedule in order to focus resources more efficiently. The method helps Program Managers (PM):
- Understand which tasks are on the critical path to determine a completion date
- How best to manage tasks around the critical path to meet the scheduled end date
- Focus on preventing schedule slips
- Gain insight when planning work packages and tasks
Benefits of Using the Critical Path Method (CPM)
Here are a few good reasons to use the CPM method:
- Improves Planning: CPM helps plan for the future by comparing expected progress to actual progress. The data from current projects can be used to help plan for future projects.
- Helps with resource loading: CPM helps project managers put tasks in order of importance, which gives them a better idea of how and where to use resources.
- Highlights bottlenecks: When projects get stuck, valuable time is lost. Using a network diagram to show project dependencies will help you figure out which tasks can and can’t be done simultaneously so that you can plan your schedule accordingly.
Determining the Critical Path
The Critical Path is determined when analyzing a project’s schedule or network logic diagram and uses the Critical Path Method (CPM). The CPM provides a graphical view of the project, predicts the time required for the project, and shows which activities are critical to maintaining the schedule.
Critical Path Method (CPM) Development Steps
The seven (7) steps in the CPM are: [1]
- Step 1: List of all activities required to complete the project (see Work Breakdown Structure (WBS)),
- Step 2: Determine the sequence of activities
- Step 3: Draw a network diagram
- Step 4: Determine the time that each activity will take to completion
- Step 5: Determine the dependencies between the activities
- Step 6: Determine the critical path
- Step 7: Update the network diagram as the project progresses
The CPM calculates the longest path of planned activities to the end of the project and the earliest and latest that each activity can start and finish without making the project longer. This process determines which activities are “critical” (i.e., on the longest path) and which have “total float” (i.e., can be delayed without making the project longer). [1]
Example of Using the Critical Path Method (CPM) to Build a Backyard Deck
The Critical Path Method (CPM) is a technique that allows you to identify tasks that are necessary for project completion and determine the minimum time required to finish the project. It also helps you to manage task dependencies and avoid delays².
To use the CPM for building a backyard deck, you need to follow these steps:
- Step 1: List all the activities or tasks required to complete the project, such as measuring, cutting, assembling, painting, etc.
- Step 2: Estimate the duration of each activity or task, based on the resources available and the complexity of the work.
- Step 3: Identify the dependencies between the activities or tasks, such as which ones need to be done before or after others.
- Step 4: Draw a network diagram that shows the sequence and dependencies of the activities or tasks, using nodes to represent activities and arrows to represent dependencies.
- Step 5: Calculate the earliest start time (ES), earliest finish time (EF), latest start time (LS), and latest finish time (LF) for each activity or task, using the forward and backward pass methods.
- Step 6: Calculate the total float (TF) or slack for each activity or task, which is the difference between the LF and EF or between the LS and ES. The float represents how much activity can be delayed without affecting the project completion time. (See Below)
- Step 7: Identify the critical path, the longest path in the network diagram with zero float. The critical path determines the minimum completion time of the project, and any delay in any activity on this path will delay the entire project.
Here is an example of using the CPM for building a backyard deck:
| Activity | Description | Duration | Predecessor |
| A | Measure and mark the deck area | 1 Hour | None |
| B | Dig holes for posts | 2 Hours | A |
| C | Cut posts to size | 1 Hour | None |
| D | Set posts in concrete | 3 Hours | B, C |
| E | Cut joists and beams | 2 Hours | None |
| F | Attach joists and beams to posts | 4 Hours | D, C |
| G | Cut and install decking boards | 6 Hours | F |
| H | Sand and stain the deck | 4 Hours | G |
The table below shows the calculations for ES, EF, LS, LF, and TF for each activity:
| Activity | ES | EF = ES + Duration | LS | LF = LS + Duration | TF = LF – EF |
| A | 0 | 1 = 0 + 1 | 0 | 1 = 0+ 1 | 0 |
| B | 1 = Max(1) | 3 = 1 + 2 | 1 = max(1) | 3 = 1 + 2 | 0 |
| C | 0 = Max(0) | 3 = 1 + 2 | 1 = max(1) | 3 = 2 + 1 | 2 |
| D | 3 = Max(3.1) | 6 = 3 + 3 | 3 = max(3,3) | 6 = 3 +3 | 0 |
| E | 0 = Max(0) | 2=0+2 | 4=max(4) | 6=4+2 | 4 |
| F | 6 = Max(6) | 10=6+4 | 6=max(6) | 10=6+4 | 0 |
| G | 10 = Max(10) | 16=10+6 | 10=max(10) | 16=10+6 | 0 |
| H | 16 = Max(16) | 20=16+4 | 16=max(16) | 20=16+4 | 0 |
The critical path for this example is A-B-D-F-G-H, with a minimum completion time of **20 hours**. Any delay in any of these activities will delay the entire project. The activities C and E have some float, which means they can be delayed without affecting the project completion time.
Calculate Float Time in the Critical Path Method (CPM)
Float time, also known as slack time, is the amount of time that a task can be delayed without affecting the start of the next task or the project completion date³. Float time can be calculated for each task using the following formulas:
- Total float: This is the difference between the latest finish time and the earliest finish time of a task, or between the latest start time and the earliest start time of a task. The formula for total float is TF = LF – EF or $TF = LS – ES where LF is the latest finish time, EF is the earliest finish time, LS is the latest start time, and ES is the earliest start time.
- Free float: This is the difference between the earliest finish time of a task and the earliest start time of the next task. The formula for free float is FF = ES – EF, where ES is the earliest start time of the next task, and EF is the earliest finish time of the current task.
To calculate float time, you need first to find the earliest and latest start and finish times for each task using a network diagram and a forward and backward pass method. Then, you can use the formulas above to find each task’s total and free float. Tasks with zero total float are on the critical path and cannot be delayed without affecting the project duration. Tasks with positive total float are not on the critical path and have some flexibility in their scheduling.
Difference Between Critical Chain Method (CCM) and Critical Path Method (CPM)
There are a few differences between the Critical Chain Method (CCM) and the Critical Path Method (CPM), but they both focus on schedule development and estimation. These are:
- Critical Path Method is focused on how long a project is based upon task estimation and the amount of float on a project.
- Critical Chain Method operates on shortening how long a project is due to overestimation, uncertainties, and buffers.
Critical Path Method (CPM) and Program Evaluation and Review Technique (PERT)
Program Evaluation and Review Technique (PERT) is a method used to examine the tasks in a schedule and determine a Critical Path Method variation (CPM). It analyzes the time required to complete each task and its associated dependencies to determine the minimum time to complete a project. It estimates the shortest possible time each activity will take, the most likely length of time, and the longest time that might be taken if the activity takes longer than expected.
Although CPM and PERT are conceptually similar, some significant differences exist mostly due to the type of projects best suited for each technique. PERT is better to use when there is much uncertainty and when control over time outweighs control over costs. PERT handles uncertainty of the time required to complete an activity by developing three estimates and then computing an expected time using the beta distribution. CPM is better suited for well-defined projects and activities with little uncertainty, where accurate time and resource estimates can be made. The percentage of completion of the activity can be determined. [1]
Critical Path Method History
The CPM scheduling technique was introduced at approximately the same time as PERT Analysis. It was developed by J. E. Kelly of Remington-Rand and M. R. Walker of DuPont to aid in scheduling maintenance shutdowns in chemical processing plants. Over the years, CPM has enjoyed more use than any other network scheduling technique. It is based on the concept of critical path and was designed to focus on the time and resources, particularly cost, necessary to complete a project’s activities.
AcqLinks and References:
- [1] Defense Systems Management College “Scheduling Guide for Program Managers” – Oct 2001
- Website: Project Manager.com – Ultimate Guide to the Critical Path Method
Updated: 7/13/2023
Rank: G9.3