A Pairwise Comparison is the process of comparing candidates in pairs to judge which of each candidate is preferred overall. Each candidate is matched head-to-head (one-on-one) with each of the other candidates. Each candidate gets 1 point for a one-on-one win and half a point for a tie. The candidate with the most total points is the winner. Pairwise comparison is a great way to help make decisions when there are many options to think about. Instead of asking someone to rank 50 different options from most important to least important, Pairwise Comparison asks them to choose between two options, A and B. This is a much simpler way to determine each option’s importance. The development of a Pairwise Matrix sometimes represents the comparison.
Definition: Pairwise comparison is a method of comparing entities in pairs to judge which one is preferred.
When is a Pairwise Comparison Used
A Pairwise Comparison is mostly used in scientific studies, voting systems, social choice, public choice, and requirements engineering. Product development teams often use pairwise to decide which features to build first, which customer needs to be given the most attention, or to narrow down ideas during brainstorming and design thinking sprints.
Conducting a Pairwise Comparison
Below is an example of the process of developing a Pairwise Comparison
Develop a Pairwise Matrix
- Each of the squares in the matrix at right represents the pairing of two items (where the numbers intersect).
- In this example, the list includes five items; the top square (shaded) represents the pairing of item 1 with item 2.
Rank each pair of items
- For each pair of items, the team should reach a consensus on which of the two items is preferred over the other.
- As the team completes each of the comparisons, the number of the preferred item is recorded in that square, until the matrix is completely filled in.
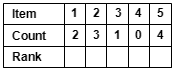
Count the number of times each item appears in the matrix.
- Using the filled-in matrix (on the far right above), count how many times each item is listed in the matrix, and record the totals in the ranking matrix (at right).
Rank all of the Items
- Rank the items based on how many times they appear in the matrix.
- To break a tie between two items appearing the same number of times, look at the square in the matrix where the two were compared; the item appearing in that box receives the higher ranking.
Another Example of a Pairwise Comparison
Sure, I can provide an example of a pairwise comparison. A pairwise comparison is a method of expressing a preference between two mutually distinct alternatives¹. It can be used to rank candidates in pairs to judge which candidate is preferred overall¹. For example, suppose you have four candidates: A, B, C, and D. You can compare them in pairs using a scale like this:
- Much better than
- Better than
- As good as
- Worse than
- Much worse than
Then, you can create a pairwise comparison matrix like this:
| A | B | C | D | |
| A | A is better than B | A is much better than C | A is good as D | |
| B | B is worse than A | B is better than C | B is worse than D | |
| C | C is much worse than A | C is much worse than D | ||
| D | D is as good as A | D is better than B | D is much better than C |
To calculate the total scores of each candidate, you can assign numerical values to each preference, such as:
- Much better than = 2
- Better than = 1
- As good as = 0
- Worse than = -1
- Much worse than = -2
Then, you can add up the scores across each row. For example, the score for A is 1 + 2 + 0 = 3. The scores for the other candidates are:
- B = -1 + 1 – 1 = -1
- C = -2 – 1 – 2 = -5
- D = 0 + 1 + 2 = 3
The final ranking of the candidates based on the pairwise comparison is:
- A and D (tied for first place with a score of 3)
- B (second place with a score of -1)
- C (last place with a score of -5)
AcqLinks and References:
- DAU Program Managers Guide
Updated: 7/13/2023
Rank: G5.1